This is a sequel to this topic where we have recalled several properties of the stereographic projection 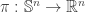 . Recall that by the following transformation
. Recall that by the following transformation
we know that
and
are equivalent in the weak sense.
The way to see it comes from the following identities
and
where 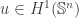 .
.
Now, we would like to mention the fact that this projection can be used to classify solutions to the following fourth-order elliptic equation coming from the 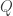 -curvature problem
-curvature problem
on the 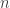 -sphere
-sphere 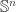 where
where
and 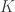 is a given function defined on
is a given function defined on 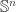 . To be exact, up to a constant, the following function
. To be exact, up to a constant, the following function
will solve the PDE where
Similarly, the following function
will solve the following PDE
on the 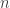 -sphere.
-sphere.

No comments:
Post a Comment