In Cartesian coordinates 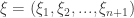 on the sphere
on the sphere 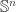 and
and 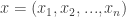 on the plane, the projection and its inverse are given by the formulas
on the plane, the projection and its inverse are given by the formulas
and
It is not hard to see that
Now we use the trick introduced in this entry. Let
and let
The determinant we are trying to compute is
which is the characteristic polynomial of 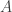 evaluated at
evaluated at 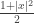 times
times 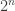 .
.
Now, 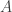 is certainly diagonalizable (which doesn’t even matter, but it makes it easier to think about), and we know its eigenvalues. Why do we know its eigenvalues? Because
is certainly diagonalizable (which doesn’t even matter, but it makes it easier to think about), and we know its eigenvalues. Why do we know its eigenvalues? Because 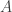 is a matrix of rank
is a matrix of rank 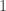 , hence nullity
, hence nullity 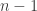 , hence
, hence 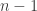 of its
of its 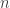 eigenvalues are zero. What is the other eigenvalue? It’s the same as the sum of the eigenvalues, which is the trace of
eigenvalues are zero. What is the other eigenvalue? It’s the same as the sum of the eigenvalues, which is the trace of 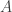 , which is
, which is 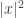 . Put that information together, and we have that the characteristic polynomial of
. Put that information together, and we have that the characteristic polynomial of 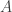 is
is
Substitute 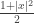 for
for 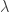 to get
to get
which implies
Thus
which implies

No comments:
Post a Comment