Showing posts with label Maths. Show all posts
Showing posts with label Maths. Show all posts

Stereographic Projection

In geometry, the stereographic projection, usually denoted by 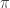\pi, is a particular mapping (function) that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point – the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it preserves angles. It is neither isometric nor area-preserving: that is, it preserves neither distances nor the areas of figures.
Intuitively, then, the stereographic projection is a way of picturing the sphere as the plane, with some inevitable compromises. Because the sphere and the plane appear in many areas of mathematics and its applications, so does the stereographic projection; it finds use in diverse fields including complex analysis, cartography, geology, and photography. In practice, the projection is carried out by computer or by hand using a special kind ofgraph paper called a stereonet or Wulff net.
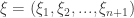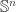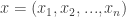In Cartesian coordinates  \xi=(\xi_1, \xi_2,...,\xi_{n+1}) on the sphere \mathbb S^n and x=(x_1,x_2,...,x_n) on the plane, the projection 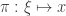\pi : \xi \mapsto x and its inverse 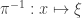\pi^{-1}: x \mapsto \xi are given by the formulas
\displaystyle\xi _i = \begin{cases} \dfrac{{2{x_i}}}{{1 + {{\left| x \right|}^2}}},&1 \leqslant i \leqslant n, \hfill \\ \dfrac{{{{\left| x \right|}^2} - 1}}{{1 + {{\left| x \right|}^2}}},&i = n + 1. \hfill \\ \end{cases}
and
\displaystyle {x_i} = \frac{{{\xi _i}}}{{1 - {\xi _{n + 1}}}}, \quad 1 \leqslant i \leqslant n.
Let us show you an example making use of the projection. We assume 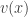v(x) verifies the following PDE
\displaystyle -\Delta v = \frac{n(n-2)}{4}v^\frac{n+2}{n-2} \quad \text{ on } \mathbb R^n.
Then the transformed function 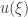u(\xi), to be exact 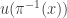u(\pi^{-1}(x)), given by
\displaystyle v(x)=u(\pi^{-1}(x))\left( \frac{2}{1+|x|^2}\right)^\frac{n-2}{2}
satisfies the following PDE
\displaystyle -\Delta_g u + \frac{n(n-2)}{4}u = \frac{n(n-2)}{4}u^\frac{n+2}{n-2} \quad \text{ on } \mathbb S^n.
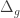where \Delta_g denotes the Laplace-Beltrami operator with respect to the standard metric 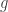g on \mathbb S^n.
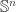Similarly, if function 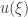u(\xi) verifying the PDE
\displaystyle -\Delta_g u + \frac{n(n-2)}{4}u = \frac{n(n-2)}{4}u^\frac{n+2}{n-2} \quad \text{ on } \mathbb S^n
then a new function 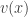v(x) given by
\displaystyle v(x)=u(\pi(x))\left( \frac{2}{1+|x|^2}\right)^\frac{n-2}{2}
will satisfy the following PDE
\displaystyle -\Delta v = \frac{n(n-2)}{4}v^\frac{n+2}{n-2} \quad \text{ on } \mathbb R^n.
More general, PDE
\displaystyle -\Delta_g u(\xi) + \frac{n(n-2)}{4}u(\xi) = K(\xi)u(\xi)^\frac{n+2}{n-2} \quad \text{ on } \mathbb S^n
becomes
\displaystyle -\Delta v(x) = K(\pi^{-1}(x))v(x)^\frac{n+2}{n-2} \quad \text{ on } \mathbb R^n.
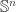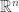In conclusion, using the stereographic projection we can transfer some geometric problems on sphere \mathbb S^n to ones in the whole space \mathbb R^n.
No comments:
Nhãn:

Stereographic Projection, 2

This is a sequel to this topic where we have recalled several properties of the stereographic projection \pi : \mathbb S^n \to \mathbb R^n. Recall that by the following transformation
\displaystyle v(x)=u(\pi^{-1}(x))\left( \frac{2}{1+|x|^2}\right)^\frac{n-2}{2}, \quad x \in \mathbb R^n
we know that
\displaystyle -\Delta_g u(\xi) + \frac{n(n-2)}{4}u(\xi) = K(\xi)u(\xi)^\frac{n+2}{n-2} \quad \text{ on } \mathbb S^n
and
\displaystyle -\Delta v(x) = K(\pi^{-1}(x))v(x)^\frac{n+2}{n-2} \quad \text{ on } \mathbb R^n
are equivalent in the weak sense.
The way to see it comes from the following identities
\displaystyle \int_{{\mathbb{S}^n}} {|\nabla u(\xi ){|^2} + \frac{{n(n - 2)}}{4}u{{(\xi )}^2} = \int_{{\mathbb{R}^n}} {|\nabla v(x){|^2}} }
and
\displaystyle \int_{{\mathbb{S}^n}} {|u(\xi ){|^{\frac{{2n}}{{n - 2}}}} = \int_{{\mathbb{R}^n}} {|v(x){|^{\frac{{2n}}{{n - 2}}}}} }
where u \in H^1(\mathbb S^n).
Now, we would like to mention the fact that this projection can be used to classify solutions to the following fourth-order elliptic equation coming from the Q-curvature problem
\Delta^2u-c_n\Delta u+d_nu=Ku^\frac{n+4}{n-4}
on the n-sphere \mathbb S^n where
c_n =\frac{1}{2}(n^2-2n-4), \quad d_n=\frac{n-4}{16}n(n^2-4)
and K is a given function defined on \mathbb S^n. To be exact, up to a constant, the following function
\displaystyle\frac{{{\beta _n}}}{{{2^{\frac{{n - 4}}{2}}}}}{\left( {\frac{\lambda }{{1 + \frac{{{\lambda ^2} - 1}}{2}(1 - \cos d(x,a))}}} \right)^{\frac{{n - 4}}{2}}}
will solve the PDE where
\displaystyle {\beta _n} = {\left( {(n - 4)(n - 2)n(n + 2)} \right)^{\frac{{n - 4}}{8}}}.
Similarly, the following function
\displaystyle {c_n}{\left( {\frac{\lambda }{{{\lambda ^2} + 1 + (1 - {\lambda ^2})\cos d(x,a)}}} \right)^{\frac{{n - 2}}{2}}}
will solve the following PDE
\displaystyle - \Delta u + \frac{{n(n - 2)}}{4}u + K{u^{\frac{{n + 2}}{{n - 2}}}} = 0
on the n-sphere.
No comments:
Nhãn:

Stereographic Projection, 3

In Cartesian coordinates  \xi=(\xi_1, \xi_2,...,\xi_{n+1}) on the sphere \mathbb S^n and x=(x_1,x_2,...,x_n) on the plane, the projection and its inverse are given by the formulas
\displaystyle\xi _i = \begin{cases} \dfrac{{2{x_i}}}{{1 + {{\left| x \right|}^2}}},&1 \leqslant i \leqslant n, \hfill \\ \dfrac{{{{\left| x \right|}^2} - 1}}{{1 + {{\left| x \right|}^2}}},&i = n + 1. \hfill \\ \end{cases}
and
\displaystyle {x_i} = \frac{{{\xi _i}}}{{1 - {\xi _{n + 1}}}}, \quad 1 \leqslant i \leqslant n.
It is not hard to see that
\displaystyle\frac{{\partial ({\xi _1},...,{\xi _n})}}{{\partial ({x_1},...,{x_n})}} = \frac{2^n}{{{{\left( {1 + {{\left| x \right|}^2}} \right)}^{2n}}}}\det \left( {\begin{array}{*{20}{c}} {1 + {{\left| x \right|}^2} - 2x_1^2}&{ - 2{x_1}{x_2}}& \cdots &{ - 2{x_1}{x_n}} \\ { - 2{x_2}{x_1}}&{1 + {{\left| x \right|}^2} - 2x_2^2}& \cdots &{ - 2{x_2}{x_n}} \\ \vdots & \vdots & \ddots & \vdots \\ { - 2{x_n}{x_1}}&{ - 2{x_n}{x_2}}& \cdots &{1 + {{\left| x \right|}^2} - 2x_n^2} \end{array}} \right).
Now we use the trick introduced in this entry. Let
\displaystyle x = \left( {\begin{array}{*{20}{c}} {{x_1}} \\ \vdots \\ {{x_n}} \end{array}} \right)
and let
A=xx^T.
The determinant we are trying to compute is
\displaystyle\det \left( {(1 + |x{|^2})I - 2A} \right) = {2^n}\det \left( {\frac{{1 + |x{|^2}}}{2}I - A} \right),
which is the characteristic polynomial of A evaluated at \frac{1+|x|^2}{2} times 2^n.
Now, A is certainly diagonalizable (which doesn’t even matter, but it makes it easier to think about), and we know its eigenvalues. Why do we know its eigenvalues? Because A is a matrix of rank 1, hence nullity n-1, hence n-1 of its n eigenvalues are zero. What is the other eigenvalue? It’s the same as the sum of the eigenvalues, which is the trace of A, which is |x|^2. Put that information together, and we have that the characteristic polynomial of A is
\displaystyle \det(\lambda I-A)=\left(\lambda-|x|^2\right)\lambda^{n-1}=\lambda^n-|x|^2\lambda^{n-1}.
Substitute \frac{1+|x|^2}{2} for \lambda to get
\displaystyle\det \left( {\frac{{1 + |x{|^2}}}{2}I - A} \right) = {\left( {\frac{{1 + |x{|^2}}}{2}} \right)^{n - 1}}\left( {\frac{{1 + |x{|^2}}}{2} - |x{|^2}} \right) = \frac{{1 - |x{|^2}}}{2}{\left( {\frac{{1 + |x{|^2}}}{2}} \right)^{n - 1}}
which implies
\displaystyle\det \left( {(1 + |x{|^2})I - 2A} \right) = (1 - |x{|^2}){(1 + |x{|^2})^{n - 1}}.
Thus
\displaystyle\det \left( {\begin{array}{*{20}{c}} {1 + {{\left| x \right|}^2} - 2x_1^2} & { - {x_1}{x_2}} & \cdots & { - {x_1}{x_n}} \\ { - {x_2}{x_1}} & {1 + {{\left| x \right|}^2} - 2x_2^2} & \cdots & { - {x_2}{x_n}} \\ \vdots & \vdots & \ddots & \vdots \\ { - {x_n}{x_1}} & { - {x_n}{x_2}} & \cdots & {1 + {{\left| x \right|}^2} - 2x_n^2} \\ \end{array} } \right) = (1 - |x{|^2}){(1 + |x{|^2})^{n - 1}}
which implies
\displaystyle\frac{{\partial ({\xi _1},...,{\xi _n})}}{{\partial ({x_1},...,{x_n})}} = {\left( {\frac{2}{{1 + {{\left| x \right|}^2}}}} \right)^n}\frac{{1 - |x{|^2}}}{{1 + |x{|^2}}}.
No comments:
Nhãn:
Subscribe to: Posts (Atom)