My Blog: Anh-Tourguide: Definition Of Coercivity

This is a classical question: how could we understand the coercivity of the operator 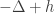$-\Delta + h$ ? Given a smooth compact Riemannian manifold of dimension 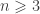$n\geqslant 3$ , the original definition for the coercivity of such an operator is just

$\displaystyle\int_M {({{\left| {\nabla u} \right|}^2} + h{u^2})d{v_g}} \geqslant C\underbrace {\int_M {({{\left| {\nabla u} \right|}^2} + {u^2})d{v_g}} }_{\left\| u \right\|_{{H^1}}^2}$

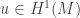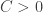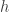for any $u \in H^1(M)$ for some constant $C>0$ . If $h$ is a function, by taking a positive constant we immediately see that it is necessary

$\displaystyle \int_M h dv_g >0$ .

Consequently, 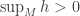$\sup_M h>0$ and in particular if 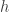$h$ is constant, 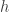$h$ must be positive. If 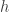$h$ is not constant, then it is not clear to classify 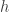$h$ . In that case, we interpret this terminology in a different manner as follows

$\displaystyle\mu=\mathop {\inf }\limits_{u \in {H^1}(M)} \frac{{\displaystyle\int_M {({{\left| {\nabla u} \right|}^2} + h{u^2})d{v_g}} }}{{\displaystyle\int_M {{u^2}d{v_g}} }} > 0.$

It is simple to show that the coercivity of 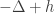$-\Delta + h$ is equivalent to 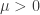$\mu>0$ . The fact that 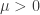$\mu>0$ implies that the coercivity of 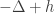$-\Delta + h$ is simple just by definition. For the reverse case, it involves a bit of calculus of variation. For interested reader, we refer to a book by O. Druet, E. Hebey, and F. Robert

Home

Đăng Tin Rao Vặt

Đăng Nhập

Đăng Ký

Thế Giới Rao Vặt 24h

Definition Of Coercivity

No comments:

Post a Comment