My Blog: Anh-Tourguide: Differentiability Via Weird Argument

Question. Suppose that 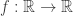$f:\mathbb R \to \mathbb R$ is such that 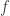$f$ is continuous and 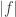$|f|$ is differentiable. Should 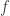$f$ also be differentiable?

Proof. Let 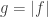$g=|f|$ . Since 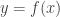$y=f(x)$ satisfies the differentiable equation

$y^2=g(x)^2$ ,

$f$ is differentiable at all points with $f(x) \neq 0$ by the implicit function theorem and

$2yy'=2gg'$ ,

and

$\displaystyle f'(x)=\frac{g(x)g'(x)}{f(x)}$ .

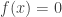Where $f(x)=0$ , we note that 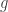$g$ has a minimum and 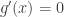$g'(x)=0$ . This gives

$\displaystyle\lim_{t\to 0}\left|\frac{f(x+t)}{t}\right|=0$

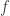and $f$ is differentiable by the definition.

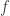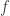Comment. The only points of interests are the zeros of $f$ since $f$ has the same sign in some neighborhood of points which are not roots. So there goes half the work. Geometrically it doesn’t make sense for 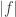$|f|$ to have anything but derivative 0 at roots of 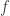$f$ and this can be verified by taking left hand and right hand limits of the quotient.

Home

Đăng Tin Rao Vặt

Đăng Nhập

Đăng Ký

Thế Giới Rao Vặt 24h

Differentiability Via Weird Argument

No comments:

Post a Comment