In the topic we showed that for any irrational 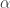 the limit
the limit
does not exist. In this topic, we consider the following limit
To be precise, we prove that
for almost every ![x \in [0,2\pi] x \in [0,2\pi]](https://s-ssl.wordpress.com/latex.php?latex=x+%5Cin+%5B0%2C2%5Cpi%5D&bg=ffffff&fg=333333&s=0) .
.
Solution. Let
Then 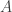 is a measurable set of measure
is a measurable set of measure 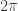 . Moreover, for any
. Moreover, for any 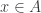 ,
,
Indeed for any 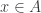 , since
, since
is dense subgroup of 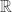 there are sequences
there are sequences 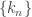 and
and 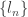 of
of 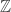 such that
such that
Since
Otherwise 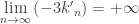 and
and

No comments:
Post a Comment