My Blog: Anh-Tourguide: Integral Calculus

Question: If the integral

$\displaystyle \int_0^\infty f (x)dx$

converges and a function 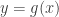$y = g(x)$ is bounded then the integral

$\displaystyle \int_0^\infty f (x)g(x)dx$

converge.

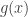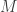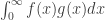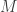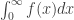Observation: It seems since $g(x)$ is bounded by a constant called $M$ , the integral $\int_0^\infty f (x)g(x)dx$ is then dominated by $M$ times $\int_0^\infty f (x)dx$ which becomes a finite number.

Counter-example: The integral

$\displaystyle \int_0^\infty \frac{\sin x}{x}dx$

converges and the function 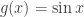$g(x)=\sin x$ is bounded but the integral

$\displaystyle \int_0^\infty \frac{\sin^2 x}{x}dx$

diverges.

Explanation: What we thought is the following estimate

$\displaystyle\left| {\int_0^\infty {f(x)g(x)dx} } \right| \leqslant \int_0^\infty {\left| {f(x)g(x)} \right|dx} \leqslant M\int_0^\infty {|f(x)|dx}$ .

However, the convergence of 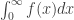$\int_0^\infty f (x)dx$ is not sufficient to imply that $\int_0^\infty |f (x)|dx<\infty$ .

Home

Đăng Tin Rao Vặt

Đăng Nhập

Đăng Ký

Thế Giới Rao Vặt 24h

Integral Calculus

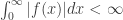No comments:

Post a Comment