In this topic, we proved a very interesting property involving the Laplacian of the Kelvin transform of a function. Recall that, for a given function  , its Kelvin transform is defined to be
, its Kelvin transform is defined to be
We then have
where the inversion point 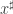 of
of  is defined to be
is defined to be
Therefore, the Kelvin transform can be defined to be
We also have another formula
The right hand side of the above identity involves 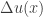 , we can rewrite this one in terms of
, we can rewrite this one in terms of 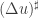 . Actually, we have the following
. Actually, we have the following
which gives
Today, we study the a more general form of the Kelvin transform. The above definition of the Kelvin transform is with respect to the origin and unit ball in 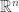 . We are now interested in the case when the Kelvin transform is defined with respect to a fixed ball. The following result is adapted from a paper due to M.C. Leung published in Math. Ann. in 2003.
. We are now interested in the case when the Kelvin transform is defined with respect to a fixed ball. The following result is adapted from a paper due to M.C. Leung published in Math. Ann. in 2003.
Define the reflection on the sphere with center at 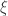 and radius
and radius 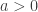 by
by
It is direct to check that
We observe that
The Kelvin transform with center at 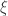 and radius
and radius 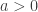 of a function
of a function  is given by
is given by
We remark that if 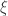 and
and  are fixed, and if
are fixed, and if 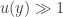 , then
, then 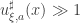 as well, where
as well, where 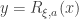 . In addition,
. In addition, 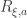 sends a set of small diameter not too close to
sends a set of small diameter not too close to 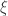 to a set of small diameter. We verify that double Kelvin transform is the identity map. We have
to a set of small diameter. We verify that double Kelvin transform is the identity map. We have

No comments:
Post a Comment