My Blog: Anh-Tourguide: Some Operations On The Hölder Continuous Functions

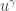This entry devotes the following fundamental question: if $u$ is Hölder continuous, then how about $u^\gamma$ for some constant 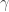$\gamma$ ? Throughout this entry, we work on 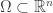$\Omega \subset \mathbb R^n$ which is not necessarily bounded.

Firstly, we have an elementary result

Proposition. If $f$ and $g$ are $\alpha$ -Hölder continuous and bounded, so is $fg$ .

Proof. The proof is simple, we just observe that

$\displaystyle\left| {f(x)g(x) - f(y)g(y)} \right| \leqslant \left| {f(x) - f(y)} \right||g(x)| + \left| {g(x) - g(y)} \right||f(y)|$

which yields

$\displaystyle\frac{{\left| {f(x)g(x) - f(y)g(y)} \right|}}{{{{\left| {x - y} \right|}^\alpha }}} \leqslant \frac{{\left| {f(x) - f(y)} \right|}}{{{{\left| {x - y} \right|}^\alpha }}}\left( {\mathop {\sup }\limits_\Omega |g(x)|} \right) + \frac{{\left| {g(x) - g(y)} \right|}}{{{{\left| {x - y} \right|}^\alpha }}}\left( {\mathop {\sup }\limits_\Omega |f(y)|} \right)$ .

Consequently,

for any positive integer number $n$ and any $\alpha$ -Hölder continuous and bounded function $u$ , function $u^n$ is also $\alpha$ -Hölder continuous and bounded.

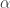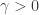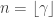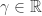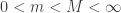Let us assume , $u$ is $\alpha$ -Hölder continuous and bounded, $\gamma>0$ is a constant. Let $n =\left\lfloor \gamma \right\rfloor$ . Since $\gamma \in \mathbb R$ , we may assume $u$ is also bounded away from zero, that means there exist two constants $0<m<M<\infty$ such that

$m<u(x)<M \quad \forall x \in \Omega$ .

We now study the 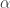$\alpha$ -Hölder continuity of 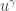$u^\gamma$ . Observe that function

$\displaystyle f(t) = {t^{\left\lceil \gamma \right\rceil }}, \quad t>0$

is sub-additive in the sense that

$\displaystyle f(t_1+t_2) \leqslant f(t_1)+f(t_2), \quad \forall t_1,t_2>0$ .

Indeed, by dividing both sides by 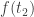$f(t_2)$ we arrive at

$\displaystyle {\left( {1 + \frac{{{t_1}}}{{{t_2}}}} \right)^{\left\lceil \gamma \right\rceil }} \leqslant 1 + {\left( {\frac{{{t_1}}}{{{t_2}}}} \right)^{\left\lceil \gamma \right\rceil }}$ .

Since

${\left\lceil \gamma \right\rceil } \leqslant 1$

the above inequality comes from the Bernoulli inequality. Therefore if there are some 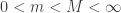$0<m<M<\infty$ then

$\displaystyle {({t_1} + {t_2})^{1 - \left\lceil \gamma \right\rceil }}{\left( {{t_1} + {t_2}} \right)^{\left\lceil \gamma \right\rceil }} = {\left( {{t_1} + {t_2}} \right)^1} \leqslant t_1^1 + t_2^1 = t_1^{\left\lceil \gamma \right\rceil }t_1^{1 - \left\lceil \gamma \right\rceil } + {t_2}$

holds for any 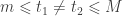$m\leqslant t_1 \ne t_2 \leqslant M$ . We now arrive at

$\displaystyle {\left( {{t_1} + {t_2}} \right)^{\left\lceil \gamma \right\rceil }} \leqslant {\left( {\frac{{{t_1}}}{{{t_1} + {t_2}}}} \right)^{1 - \left\lceil \gamma \right\rceil }}t_1^{\left\lceil \gamma \right\rceil } + \frac{1}{{{{({t_1} + {t_2})}^{1 - \left\lceil \gamma \right\rceil }}}}{t_2} \leqslant t_1^{\left\lceil \gamma \right\rceil } + \frac{1}{{{{(2m)}^{1 - \left\lceil \gamma \right\rceil }}}}{t_2}$ .

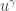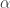We now make use the above estimate to show that $u^\gamma$ is $\alpha$ -Hölder continuous. Indeed, we have the following

$\displaystyle \left| {u{{(x)}^{\left\lceil \gamma \right\rceil }} - u{{(y)}^{\left\lceil \gamma \right\rceil }}} \right| \leqslant \frac{1}{{{{(2m)}^{1 - \left\lceil \gamma \right\rceil }}}}\left| {u(x) - u(y)} \right|$ .

Consequently, we get

$\displaystyle \frac{{\left| {u{{(x)}^{\left\lceil \gamma \right\rceil }} - u{{(y)}^{\left\lceil \gamma \right\rceil }}} \right|}}{{{{\left| {x - y} \right|}^\alpha }}} \leqslant \frac{1}{{{{(2m)}^{1 - \left\lceil \gamma \right\rceil }}}}\frac{{\left| {u(x) - u(y)} \right|}}{{{{\left| {x - y} \right|}^\alpha }}} < \infty$ .

Thus, from

$\displaystyle\frac{{\left| {u{{(x)}^\gamma } - u{{(y)}^\gamma }} \right|}}{{{{\left| {x - y} \right|}^\alpha }}} \leqslant \frac{{\left| {u{{(x)}^{\left\lfloor \gamma \right\rfloor }} - u{{(y)}^{\left\lfloor \gamma \right\rfloor }}} \right|}}{{{{\left| {x - y} \right|}^\alpha }}}\left( {\mathop {\sup }\limits_\Omega {u^{\left\lceil \gamma \right\rceil }}} \right) + \frac{{\left| {u{{(x)}^{\left\lceil \gamma \right\rceil }} - u{{(y)}^{\left\lceil \gamma \right\rceil }}} \right|}}{{{{\left| {x - y} \right|}^\alpha }}}\left( {\mathop {\sup }\limits_\Omega {u^{\left\lfloor \gamma \right\rfloor }}} \right)$

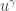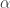we claim that $u^\gamma$ is $\alpha$ -Hölder continuous.

Let us now turn to the case 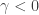$\gamma<0$ . For the sake of simplicity, let us denote 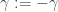$\gamma :=-\gamma$ , i.e. the function under investigating is 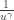$\frac{1}{u^\gamma}$ . Obviously

$\displaystyle\left| {\frac{1}{{u(x)}} - \frac{1}{{u(y)}}} \right| = \frac{{\left| {u(x) - u(y)} \right|}}{{\left| {u(x)u(y)} \right|}} \leqslant \frac{1}{{{m^2}}}\left| {u(x) - u(y)} \right|$ .

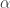Thus $\frac{1}{u}$ is $\alpha$ -Hölder continuous since

$\displaystyle\frac{{\left| {\frac{1}{{u(x)}} - \frac{1}{{u(y)}}} \right|}}{{{{\left| {x - y} \right|}^\alpha }}} \leqslant \frac{1}{{{m^2}}}\frac{{\left| {u(x) - u(y)} \right|}}{{{{\left| {x - y} \right|}^\alpha }}} < \infty$

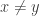for any $x\ne y$ . Consequently,

for any positive integer number $n$ and any $\alpha$ -Hölder continuous and bounded function $u$ , function $\frac{1}{u^n}$ is $\alpha$ -Hölder continuous.

Similarly, we can prove

$\displaystyle \left| {\frac{1}{{u{{(x)}^{\left\lceil \gamma \right\rceil }}}} - \frac{1}{{u{{(y)}^{\left\lceil \gamma \right\rceil }}}}} \right| \leqslant \frac{1}{{{{(2M)}^{1 - \left\lceil \gamma \right\rceil }}}}\left| {\frac{1}{{u(x)}} - \frac{1}{{u(y)}}} \right| \leqslant \frac{1}{{{{(2M)}^{1 - \left\lceil \gamma \right\rceil }}{m^{\frac{{\left\lceil \gamma \right\rceil }}{2}}}}}\left| {u(x) - u(y)} \right|$ .

Thus

$\displaystyle\frac{1}{{{u^{\left\lceil \gamma \right\rceil }}}}$

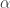is $\alpha$ -Hölder continuous. It is now easy to prove that 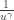$\frac{1}{u^\gamma}$ is also 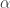$\alpha$ -Hölder continuous. So far we have proved the following

Theorem. If $u$ is $\alpha$ -Hölder continuous, positive and bounded (i.e. $u<M$ ). We assume in addition $u$ is bounded away from zero (i.e. $0<m<u$ ). Then $u^\gamma$ is also $\alpha$ -Hölder continuous for any constant $\gamma >0$ .

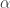The boundedness of $u$ plays an important role in our argument. In practice, if strictly positive function $u$ is locally $\alpha$ -Hölder continuous on 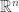$\mathbb R^n$ , we are the able to apply the theorem. We will discuss something related to this application later.

Home

Đăng Tin Rao Vặt

Đăng Nhập

Đăng Ký

Thế Giới Rao Vặt 24h

Some Operations On The Hölder Continuous Functions

No comments:

Post a Comment