My Blog: Anh-Tourguide: An Identity Of Differentiation Involving The Kelvin Transform

This short note is to prove the following

$\displaystyle {\nabla _x}\left( {u\left( {\frac{x}{{{{\left| x \right|}^2}}}} \right)} \right) \cdot x = - {\nabla _y}\left( {u\left( y \right)} \right) \cdot y$

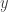where $x$ and $y$ are connected by

$\displaystyle y = \frac{x}{{{{\left| x \right|}^2}}} \in {\mathbb{R}^2}$ .

The proof is straightforward as follows.

Calculation of $\frac{\partial}{\partial x_1}$ .

We see that

$\displaystyle\begin{gathered} \frac{\partial }{{\partial {x_1}}}\left( {u\left( {\frac{x}{{{{\left| x \right|}^2}}}} \right)} \right){x_1} = \frac{\partial }{{\partial {y_1}}}\left( {u\left( y \right)} \right)\frac{\partial }{{\partial {x_1}}}\left( {\frac{{{x_1}}}{{{{\left| x \right|}^2}}}} \right){x_1} + \frac{\partial }{{\partial {y_2}}}\left( {u\left( y \right)} \right)\frac{\partial }{{\partial {x_1}}}\left( {\frac{{{x_2}}}{{{{\left| x \right|}^2}}}} \right){x_1} \hfill \\ \qquad\qquad\qquad= \frac{\partial }{{\partial {y_1}}}\left( {u\left( y \right)} \right)\left( {\frac{1}{{{{\left| x \right|}^2}}} - \frac{{2x_1^2}}{{{{\left| x \right|}^4}}}} \right){x_1} + \frac{\partial }{{\partial {y_2}}}\left( {u\left( y \right)} \right)\left( { - \frac{{2{x_1}{x_2}}}{{{{\left| x \right|}^4}}}} \right){x_1}. \hfill \\ \end{gathered}$

Calculation of $\frac{\partial}{\partial x_2}$ .

Similarly, we get

$\displaystyle\begin{gathered} \frac{\partial }{{\partial {x_2}}}\left( {u\left( {\frac{x}{{{{\left| x \right|}^2}}}} \right)} \right){x_2} = \frac{\partial }{{\partial {y_1}}}\left( {u\left( y \right)} \right)\frac{\partial }{{\partial {x_2}}}\left( {\frac{{{x_1}}}{{{{\left| x \right|}^2}}}} \right){x_2} + \frac{\partial }{{\partial {y_2}}}\left( {u\left( y \right)} \right)\frac{\partial }{{\partial {x_2}}}\left( {\frac{{{x_2}}}{{{{\left| x \right|}^2}}}} \right){x_2} \hfill \\ \qquad\qquad\qquad= \frac{\partial }{{\partial {y_1}}}\left( {u\left( y \right)} \right)\left( { - \frac{{2{x_1}{x_2}}}{{{{\left| x \right|}^4}}}} \right){x_2} + \frac{\partial }{{\partial {y_2}}}\left( {u\left( y \right)} \right)\left( {\frac{1}{{{{\left| x \right|}^2}}} - \frac{{2x_2^2}}{{{{\left| x \right|}^4}}}} \right){x_2}. \hfill \\ \end{gathered}$

Calculation of $\nabla_x \cdot x$ .

Thus

$\displaystyle\begin{gathered} {\nabla _x}\left( {u\left( {\frac{x}{{{{\left| x \right|}^2}}}} \right)} \right) \cdot x = \frac{\partial }{{\partial {y_1}}}\left( {u\left( y \right)} \right){x_1}\left( {\frac{1}{{{{\left| x \right|}^2}}} - \frac{{2x_1^2}}{{{{\left| x \right|}^4}}}} \right) + \frac{\partial }{{\partial {y_2}}}\left( {u\left( y \right)} \right){x_1}\left( { - \frac{{2{x_1}{x_2}}}{{{{\left| x \right|}^4}}}} \right) +\\ \quad\qquad\qquad \frac{\partial }{{\partial {y_1}}}\left( {u\left( y \right)} \right){x_2}\left( { - \frac{{2{x_1}{x_2}}}{{{{\left| x \right|}^4}}}} \right) + \frac{\partial }{{\partial {y_2}}}\left( {u\left( y \right)} \right){x_2}\left( {\frac{1}{{{{\left| x \right|}^2}}} - \frac{{2x_2^2}}{{{{\left| x \right|}^4}}}} \right) \hfill \\ \qquad\qquad= \frac{\partial }{{\partial {y_1}}}\left( {u\left( y \right)} \right)\left[ {\frac{{{x_1}}}{{{{\left| x \right|}^2}}} - \frac{{2x_1^3}}{{{{\left| x \right|}^4}}} - \frac{{2{x_1}x_2^2}}{{{{\left| x \right|}^4}}}} \right] + \frac{\partial }{{\partial {y_2}}}\left( {u\left( y \right)} \right)\left[ {\frac{{{x_2}}}{{{{\left| x \right|}^2}}} - \frac{{2x_2^3}}{{{{\left| x \right|}^4}}} - \frac{{2x_1^2{x_2}}}{{{{\left| x \right|}^4}}}} \right] \hfill \\ \qquad\qquad= \frac{\partial }{{\partial {y_1}}}\left( {u\left( y \right)} \right)\left[ {\frac{{{x_1}}}{{{{\left| x \right|}^2}}} - 2{x_1}\left( {\frac{{x_1^2}}{{{{\left| x \right|}^4}}} + \frac{{x_2^2}}{{{{\left| x \right|}^4}}}} \right)} \right] + \frac{\partial }{{\partial {y_2}}}\left( {u\left( y \right)} \right)\left[ {\frac{{{x_2}}}{{{{\left| x \right|}^2}}} - 2{x_2}\left( {\frac{{x_2^2}}{{{{\left| x \right|}^4}}} + \frac{{x_1^2}}{{{{\left| x \right|}^4}}}} \right)} \right] \hfill \\ \qquad\qquad= \frac{\partial }{{\partial {y_1}}}\left( {u\left( y \right)} \right)\left[ {\frac{{{x_1}}}{{{{\left| x \right|}^2}}} - \frac{{2{x_1}}}{{{{\left| x \right|}^2}}}} \right] + \frac{\partial }{{\partial {y_2}}}\left( {u\left( y \right)} \right)\left[ {\frac{{{x_2}}}{{{{\left| x \right|}^2}}} - \frac{{2{x_2}}}{{{{\left| x \right|}^2}}}} \right]. \hfill \\ \end{gathered}$

It is now easy to see that

$\displaystyle {\nabla _x}\left( {u\left( {\frac{x}{{{{\left| x \right|}^2}}}} \right)} \right) \cdot x = - {\nabla _y}\left( {u\left( y \right)} \right) \cdot y.$

The proof follows.

Home

Đăng Tin Rao Vặt

Đăng Nhập

Đăng Ký

Thế Giới Rao Vặt 24h

An Identity Of Differentiation Involving The Kelvin Transform

No comments:

Post a Comment