My Blog: Anh-Tourguide: An Identity Of Differentiation Involving The Kelvin Transform, 2

I found the following interesting identity which is similar to what I have showed recent days [here]. In that entry, we showed that

$\displaystyle {\nabla _x}\left( {u\left( {\frac{x}{{{{\left| x \right|}^2}}}} \right)} \right) \cdot x = - {\nabla _y}\left( {u\left( y \right)} \right) \cdot y$

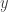where $x$ and $y$ are connected by

$\displaystyle y = \frac{x}{{{{\left| x \right|}^2}}} \in {\mathbb{R}^2}$ .

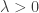For $\lambda>0$ we denote by 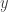$y$ the following

$\displaystyle y = \frac{\lambda^2 x}{{{{\left| x \right|}^2}}} \in {\mathbb{R}^n}$ .

Then we show that

Lemma.
$\displaystyle {\left| x \right|^2}{\Delta _x}u\left( {\frac{{{\lambda ^2}x}}{{{{\left| x \right|}^2}}}} \right) - (n - 2)x \cdot {\nabla _x}u\left( {\frac{{{\lambda ^2}x}}{{{{\left| x \right|}^2}}}} \right) = {\left| y \right|^2}{\Delta _y}u\left( y \right) - (n - 2)y \cdot {\nabla _y}u\left( y \right)$ .

Proof. Writing

$\displaystyle w(x) = {\left| x \right|^{ - \frac{{n - 2}}{2}}}u\left( {\frac{{{\lambda ^2}x}}{{{{\left| x \right|}^2}}}} \right)$

we have

$\displaystyle {\left| x \right|^{\frac{{n + 2}}{2}}}{\Delta _x}w(x) = {\left| x \right|^2}{\Delta _x}u\left( {\frac{{{\lambda ^2}x}}{{{{\left| x \right|}^2}}}} \right) - (n - 2)x \cdot {\nabla _x}u\left( {\frac{{{\lambda ^2}x}}{{{{\left| x \right|}^2}}}} \right) - \frac{{{{(n - 2)}^2}}}{4}u\left( {\frac{{{\lambda ^2}x}}{{{{\left| x \right|}^2}}}} \right)$ .

Similarly, writing

$\displaystyle W(y) = {\left| y \right|^{ - \frac{{n - 2}}{2}}}u\left( y \right)$

we have

$\displaystyle {\left| y \right|^{\frac{{n + 2}}{2}}}{\Delta _y}W(y) = {\left| y \right|^2}{\Delta _y}u\left( y \right) - (n - 2)y \cdot {\nabla _y}u\left( y \right) - \frac{{{{(n - 2)}^2}}}{4}u\left( y \right)$ .

$\displaystyle |y|=\frac{\lambda^2}{|x|}$

it follows that

$\displaystyle {\left| x \right|^{\frac{{n + 2}}{2}}}{\Delta _x}w(x) = u\left( {\frac{{{\lambda ^2}x}}{{{{\left| x \right|}^2}}}} \right) = u(y) = {\left| y \right|^{\frac{{n + 2}}{2}}}{\Delta _y}W(y) = {\left( {\frac{{{\lambda ^2}}}{{|x|}}} \right)^{\frac{{n - 2}}{2}}}W(y)$ .

Then we obtain

$\displaystyle W(y) = {\left( {\frac{{|x|}}{\lambda }} \right)^{n - 2}}w(x)$ .

By the property of the Kelvin transformation, we obtain

$\displaystyle {\Delta _y}W(y) = {\left( {\frac{{|x|}}{\lambda }} \right)^{n - 2}}{\Delta _x}w(x)$ .

Then we have

$\displaystyle {\left| x \right|^{\frac{{n + 2}}{2}}}{\Delta _x}w(x) = {\left( {\frac{{{\lambda ^2}}}{{|x|}}} \right)^{\frac{{n + 2}}{2}}}{\left( {\frac{{|x|}}{\lambda }} \right)^{n - 2}}{\Delta _x}w(x) = {\left| y \right|^{\frac{{n + 2}}{2}}}{\Delta _y}W(y)$

Home

Đăng Tin Rao Vặt

Đăng Nhập

Đăng Ký

Thế Giới Rao Vặt 24h

An Identity Of Differentiation Involving The Kelvin Transform, 2

No comments:

Post a Comment