Today, I have been asked to calculate the following limit
for each fixed ![x \in [0,2\pi] x \in [0,2\pi]](https://s-ssl.wordpress.com/latex.php?latex=x+%5Cin+%5B0%2C2%5Cpi%5D&bg=ffffff&fg=333333&s=0) . From the mathematical point of view, we can assume
. From the mathematical point of view, we can assume 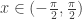 as we just replace
as we just replace  by
by 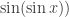 if necessary.
if necessary.
There are three possible cases
Case 1. 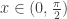 . In this case, it is well known that function
. In this case, it is well known that function 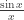 is monotone decreasing since
is monotone decreasing since
in its domain. Consequently, it holds
It turns out that
Keep in mind that
as 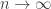 . Thus
. Thus
Case 2. 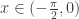 . Due to the fact that
. Due to the fact that 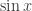 is odd with respect to
is odd with respect to  , we can replace
, we can replace  by
by 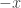 to reach to the result
to reach to the result
Case 3. 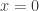 . This is trivial.
. This is trivial.
Taking into account above cases we deduce that
for any  .
.

No comments:
Post a Comment