Recently, I have learnt from my friend, ZJ, the following result
Assume thatis absolutely integrable. Then
The result seems reasonable by the following observation, for example, we consider the first identity when 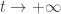 . Then the factor
. Then the factor
decays faster then the exponent function 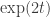 . This may be true, of course we need to prove mathematically, because the integrand contains the term
. This may be true, of course we need to prove mathematically, because the integrand contains the term 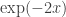 which turns out to be a good term since
which turns out to be a good term since 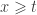 . So here is the trick in order to solve such a problem.
. So here is the trick in order to solve such a problem.
A proof of
To prove this, we split the function under the limit sign into two parts as the following
The term
can be estimated as follows
as 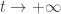 . The term
. The term
can be estimated as the following
as 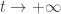 . Thus, it is clear now to see why the first identity holds.
. Thus, it is clear now to see why the first identity holds.

No comments:
Post a Comment