This entry devotes an existence result for the following semilinear elliptic equation
in the whole space 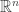 where
where 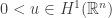 .
.
Our aim is to apply the implicit function theorem. It is known in the literature that
Theorem (implicit function theorem). Letbe Banach spaces. Let the mapping
be continuously Fréchet differentiable.
If,
andis a Banach space isomorphism fromonto
, then there exist neighborhoods
of
and
of
and a Frechet differentiable function
such that
andif and only if
, for all
.
Let us now consider
Let us define
It is not hard to see that Fréchet derivative of 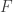 at
at 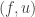 with respect to
with respect to  in the direction
in the direction  is given by
is given by
Since 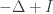 defines an isomorphism from
defines an isomorphism from 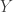 to
to 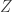 , it is clear to see that our PDE is solvable for
, it is clear to see that our PDE is solvable for 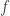 small enough in the
small enough in the 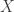 -norm.
-norm.

No comments:
Post a Comment