My Blog: Anh-Tourguide: Convergence Of Improper Integrals Does Not Imply The Integrands Go To Zero

This entry devotes a similar question that raises during a course of series. We all know that for a convergent series of (positive) real number

$\displaystyle \sum_{n=1}^\infty a_n$

it is necessary to have

$\displaystyle\mathop {\lim }\limits_{n \to \infty } {a_n} = 0$ .

This is the so-called 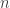$n$ -th term test. A natural extension is the following question

Question. Suppose 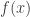$f(x)$ is positive on 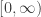$[0,\infty)$ and

$\displaystyle\int_0^{ + \infty } {f(x)dx}$

exists. Must 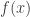$f(x)$ tend to zero as $x \to +\infty$ ?

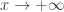I will show that this is indeed not the case. Take

$\displaystyle f(x)=\frac{1}{e^x}+g(x), \quad x \geqslant 0$

where

$\displaystyle g(x)=\begin{cases}0, & x \in \left[0,\frac{7}{4}\right], \\ 1, & x=2,3,..., \\ n^2(x-n)+1,& x \in [n-n^{-2},n], n=2,3,..., \\ -n^2(x-n)+1,& x\in [n,n+n^{-2}],n=2,3,..., \\ 0,& \text{otherwise}.\end{cases}$

The above solution tell us the fact that the convergence of improper integral 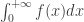$\int_0^{ + \infty } {f(x)dx}$ is not enough to guarantee $\mathop {\lim }_{x \to \infty } f(x) = 0$ .

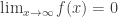It turns out to propose the question under what condition on 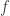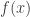$f$ , $f(x)$ tend to zero as 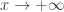$x \to +\infty$ ? There are several answers in the literature, for example

If $f$ is positive, differentiable and $|f'(x)|$ is uniformly bounded, say by $M$ , then by the mean value theorem, we can prove $\mathop {\lim }_{x \to \infty } f(x) = 0$ .
If $f$ is uniformly continuous on $[0,\infty)$ then the same conclusion still holds by the Cauchy theorem.
If $f$ is monotone decreasing, we obtain a stronger result, i.e. $\mathop {\lim }_{x \to \infty } xf(x) = 0$ .

Home

Đăng Tin Rao Vặt

Đăng Nhập

Đăng Ký

Thế Giới Rao Vặt 24h

Convergence Of Improper Integrals Does Not Imply The Integrands Go To Zero

No comments:

Post a Comment