It is clear that the implicit function theorem plays an important role in analysis. From now on, I am going to demonstrate this significant matter from the theory of differential equations, both ODE and PDE, point of view.
Let us start with the following ODE
on some domain 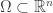 with
with 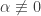 and
and 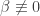 . We assume the existence result on
. We assume the existence result on 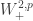 is proved for some
is proved for some 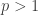 . We prove the following
. We prove the following
Theorem. The solutiondepends continuously on
.
Proof. Consider the map
taking
This map is evidently continuous (since 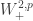 is an algebra). One readily shows that its Fréchet derivative at
is an algebra). One readily shows that its Fréchet derivative at 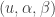 with respect to
with respect to  in the direction
in the direction 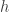 is
is
The continuity of the map
follows from the fact that 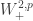 is an algebra continuously embedded in
is an algebra continuously embedded in 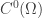 .
.
Since 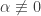 and
and 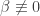 , the potential
, the potential
is not identically zero. Thus it is well-known that the map
is an isomorphism.
The implicit function theorem then implies that if 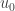 is a solution for data
is a solution for data 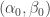 , there is a continuous map defined near
, there is a continuous map defined near 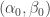 taking
taking 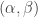 to the corresponding solution of the ODE. This establishes the conclusion.
to the corresponding solution of the ODE. This establishes the conclusion.

No comments:
Post a Comment