This note is to concern a recent result by David G. Costa [here]. Here the statement
Theorem 1.1. For alland
one has
where. In addition, if
, then
where the constantis sharp.
Here’s the proof.
Proof. For all 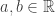 and
and 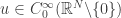 one has, for all
one has, for all 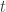 , the following
, the following
Expanding the above yields
If we denote the last integral by 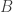 and write it as
and write it as
an integration by parts gives
Keep in mind that
A second integration by parts on the first integral above yields
so that 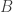 becomes
becomes
Therefore, we have
for any 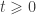 where
where 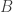 is given above and
is given above and
This is equivalent to 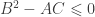 , i.e.
, i.e.
This completes the first inequality. On the other hand, since
we know that
provided 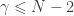 . This proves the second inequality.
. This proves the second inequality.

No comments:
Post a Comment